![]() 数学初三上 第二十四章 相似三角形
数学初三上 第二十四章 相似三角形
24.5 相似三角形的性质 第一课时(1)
名字:__________
1、选择题
1、在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,假如△ABC的周长是20,面积是12,那样△DEF的周长、面积依次为 ( )
A.10,3 B.10,6 C.5,3 D.5,6
2、如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

第2题
3、已知△ABC∽△DEF,且AB:DE=1:![]() ,则△ABC的面积与△DEF的面积之比为 ( )
,则△ABC的面积与△DEF的面积之比为 ( )
A.1:2 B.1:3 C.1:4 D.1:5
4、已知△ABC的三边长分别为20cm ,50cm,60cm,现要借助长度分别为30cm和60cm的细木条各一根,做一个三角形木架与三角形相似,需要以其中一根为一边,将另一根截成两段(允许有余料)作为另外两边.那样另两边的长度(单位:cm)分别为 ( )
A、10,25 B、12,36 C、10,25或12,36 D、10,36或12,36
5. 已知△ABC∽△DEF,且BC=4,EF=6,DE边上的中线为9,则AB边上的中线( )
A.5 B.6 C.7 D.8
6. 等边三角形的边长为6,则它的内接正方形的边长 ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、填空题
7、已知△ABC∽△DEF,且面积比为9∶25,则△ABC与△DEF的相似比为__________.
8、已知△ABC∽△DEF且周长之比为2:3,则△ABC与△DEF的面积比为 __________.
9. 若两个相似三角形的相似比是1∶3,则它们的对应高线的比是__________,对应中线的比__________,对应角平分线的比是__________,周长比是__________,面积比是__________。
10. 两个等边三角形的面积比是3∶16,则它们的边长比是__________,周长比是__________。
11、在△ABC中,DE∥BC,E、D分别在AC、AB上,EC=2AE,则S△ADE∶S四边形DBCE的比为______
12、如图, △ABC中,DE∥FG∥BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=______
13.已知:梯形ABCD中,AD∥BC,AD=32cm,BC=60cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=35cm,则OF=_______.



第12题 第13题 第14题
14、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽Δ______.它们的相似比K =_______.
3、解答卷
15. 某城市规划图的比率尺为1∶2000,图中一个绿化区的周长为24cm,面积为15cm2,则这个氯化区的实质周长和面积分别为多少?
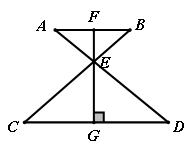
16. 如图,AB∥CD,AD与BC相交于点E,过点E作FG⊥AB,交AB于点F,交CD于点G,已知AB=7,CD=17.5,EF=4,求EG。
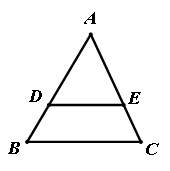
17. 如图,在△ABC中,DE∥BC,AB=7,BC=5,AC=6。
 若
若![]() =
=![]() ,求DE的长。
,求DE的长。
若![]() =
=![]() ,求DE的长。
,求DE的长。
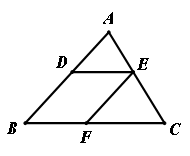
18. 如图,在△ABC中,DE∥BC,EF∥AB,已知△ADE与△EFC的面积分别为9![]() ,16
,16 ![]() ,求:
,求:![]() 。
。
19. 如图,平行四边形ABCD中,E是BC上一点,AE交BD于点F,已知BE∶EC=5∶2,![]() ,求
,求![]() .
.

 20. 如图,△ABC是一块锐角三角形余料,边BC=60毫米,高AD=40毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
20. 如图,△ABC是一块锐角三角形余料,边BC=60毫米,高AD=40毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
数学初三上 第二十四章 相似三角形
24.5 相似三角形的性质 第一课时(1)
参考答案
1. A 2. B 3. D 4.C 5. B 6. A
7. 3:5
8. 4:9
9. 1∶3 1∶3 1∶3 1∶3 1:9
10. ![]()
![]()
11. 1:8
12. 1:3:5
13. 75cm
14. ABC ![]()
15. 周长:480米,面积:6000米2
16. 10
17. (1)![]()
(2)![]() ,提示:
,提示:![]() =
=![]()
18. 49 提示: ,
,
19. 49
20. 解:设正方形PQMN是符合需要的△ABC的高AD与PN相交于点E。
设正方形PQMN的边长为x毫米。
由于PN∥BC,所以△APN∽ △ABC
所以AD=BC
∵BC=60毫米, AD=40毫米
∴![]() 得 x=24(毫米)。
得 x=24(毫米)。
所以,这个正方形零件的边长是24毫米。







